帶有非線性聯軸器軸系穩態響應計算方法的研究

5-1帶有非線性聯軸器軸系力學和數學模型的建立
在第三章，根據試驗的基礎建立了具有非線性遲滯特性聯袖器的恢復力模型。這一章，將研究一個帶有這種聯軸器的軸系如圖5-1所示，該軸系有n個圓盤，由鋼絲繩聯軸器與主機相連接，按以下原則建立力學模型：
1.每個圓盤均視為剛性勻質，所有圓盤的質量mi都有不同程度的偏心距ei。轉軸軸線垂直通過各圓盤的幾何中心；
2.設軸承、軸承座以及聯軸器各向同性，靜坐標系如圖5-1所示，支座處理成簡支；
3.聯軸器從動端處理成一集中質量m_b，由于聯軸器主動端與主機軸相連接，主機袖相對軸系軸來說，較短較粗，剛性較大，變形較小，故將聯軸器主動端、主機軸視為一體，位移為零，聯軸器從動端與主動端之間由非線性彈簧及非線性阻尼器聯結；
4.軸系為小位移振動，且忽略回轉效應。

當主機以角速度ω轉動時，軸系在各偏心力的作用下產生穩態振動，其運動微分方程可表示為：

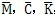
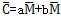
式中 分別為軸系的質量和左陣、阻尼矩陣和剛度矩陣。其中阻尼矩陣，a，b為比例常數。

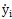
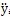
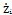
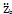
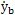
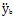
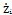
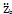
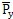
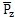
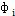
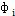
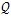
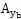
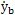
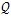
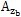
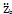
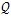
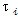
其中：y_i,z_i分別為軸系中第i個圓盤在y,z方向的位移分量； =dy_i/dt， =d²y_i/dt²， =dz_i/dt， =d²z_i/dt²分別為對應于位移分量y_i,z_i的速度和加速度，y_b,z_b為聯軸器從動端集中質量塊m_b在y,z方向的位移； =dy_b/dt， =d²y_b/dt²， =dz_i/dt， =d²z_d/dt²分別為對應于位移分量yb,zb的速度和加速度；,為y,z方向的激勵力向量，其中m_ie_iω²cos（ωt+ ），m_ie_iω²sin（ωt+ ）分別為y,z方向的偏心力分量； （ ，y_b， ，ωt), （ ，z_b， ，ωt）分別為非線性彈性聯軸器恢復力 在y,z方向的分量。 為第i個圓盤質量偏心的初相位角，即軸系靜止時，第i個圓盤質心和幾何中心連線與水平軸的夾角。
由于假設軸承、軸承座以及聯軸器各向同性，式（5-1〕、式（5-2）解法相同，只需要討論二者之一即可。

式（5-l）表示一個局部非線性彈性和阻尼元件的振動系統，對這種系統，按現有常規方法來求解是非常困難的，為此，本文以GILM為基礎發展了一種稱為SSGILM(Separate System-Gal-erkin and Improved Levenbery-Marquar-dt）的方法來求解此類微分方程組。

5-2  SSGILM法

一.振動微分方程組的改寫和解耦
首先把有局部非線性系統振動微分方程組（5-1）式改寫成只有線性常系數的微分方程組和一個具有非線性變參數的微分方程兩部分：

式中：

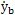
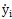
式（5-4）的P_y中含有y_b和 而（5-5）的F_j中含有y_j，（j=1，2，… n）。這樣，軸系分成運動微分方程耦聯的兩個子系統一線性軸系子系統和非線性聯軸器子系統。

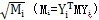
式（5-4）為線性方程，按常規方法可求出無阻尼的各階固有頻率p_i以及對應的主振型Y_i向量（i=1，2，…，n），Y_i分別除以相應廣義質量的平方根 得到正則振型Y_Ni向量。引入正則振型坐標W_Ni，對（5-4）式進行坐標變換；

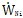
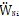
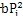
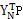
式中，W_Ni為正則振型向量W_N中的第i個分量， 和 ，分別為它對時間t的一次導數和二次導數；I為單位矩陣； s_i=（a+ ）/2P_i=c_ii/2p_im_i為振型比例阻尼比；P_Ni為P_N= P_y激勵力向量中的第i個分量。
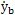
經正則坐標變換，雖然得到互不耦合的線性微分方程組（5-9)，但是（5-9）式仍然不能像單自由度振動系統那樣求解，因為（5-9）式中的激勵力包含未知的振動位移y_b和振動速度 。如果y_b已知，就可以從（5-9）式中解得W_Ni，進而可以由（5-7）式得到各y_i。因此需要求得y_b。
圖5-1所示軸系在主機帶動下轉動時，各圓盤質量偏心將產生周期偏心激勵力，根據第二章的試驗結果，聯軸器非線性恢復力Q是時間的周期函數，因此當軸系中有聯軸器這種局部非線性元件時，可以設它的位移響應是周期性的，即假設y_b有下面的形式：

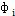
由式（5-6）、（5-8）和（5-9）可知，激勵力由二類力構成，一類是質量偏心力m_ie_iω²cos（ωt+ ，另一類是恢復力k_i（n+1）y_b-c_i（n+1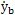） ，為求解（5-8）式方便，將（5-10）代入（5-8）式，并將正則激勵力分解成：

P_N= P_y=P_N1+P_N2                                        （5-11）

式中：

由（5-11）和（5-12）式可知，若{a}已知，就可以由（5-12）式求出各W_Ni，代W_Ni入（5-7）式，可以得到各y_i。由此可以把求y_b的問題轉化為求{a}=[a₀  a₁ 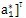 的問題。

二、Galerkin法的應用

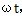
為了求出{a}，引入無量綱時間τ= ，則（5-10）式可以寫成：

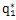
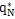
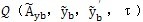
式中[q₀  q₁   … q_N  ]^T的各分量為聯軸器恢復力 的傅立葉級數各簡諧分量的系數分量。[f₁₀  f₁₁ 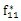   …  f_1N 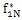   ]^T，…[f_jo  f_j1 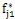  … f_jN 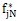 ]^T，…[f_n0  f_n1 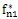  … f_nN 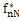 ]^T分別為彈性恢復力和阻尼恢復力的F₁=k_（n+1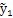） +c_（n+1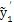） …，F_j=k_（n+1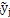）+ c_（n+1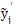） …，F_n=k_（n+1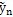）+_（n+1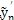） 的傅立葉級數各簡諧分量的系數向量。

由以上推導可知，求解帶有非線性聯軸器軸系的穩態響應，可以歸結為聯合求解2N+1個非線性代數方程組（5-15）和求解n個微分方程組（5-4)而重點又在于由（5-15）式求得2N

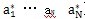
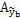
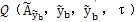
+1個未知量［a₀  a₁  ］^T。由(5-15）式可知，它不同于一般的非線性方程組，在一般的非線性方程組中，未知量是顯含的，而（5-15）式的未知量{a}是隱含的，而且{q｝是{a｝的非線件函數。不能通過將y_b的傅立葉展開式代人恢復力O的表達式中來直接求得，這是因為Q表達式中的振幅 不能表示成{a}的顯函數的緣故。因此要想由（5-1）式解得｛a}，還需要解決兩個問題：一是如何求 ,二是用什么來解隱含{a}的方程組（5-15)。下面就決這些問題。

三、ILM法

將非線性方程組簡寫成：

由于向量函數{r（{a}）}中非線性項{q（{a}）}的復雜性，可行的求解方法是采用數值法。

對于式（5-17）的數值法求解問題，我們將其轉化為與之等效的目標函數：

的極小值問題。即非線笥方程組（5-17）的解{a}可以通過求此極小值問題的最小二乘解得到。在此采用一種改進的LM算法（ILM）來求解這一問題。ILM法的基本思想簡述如下：

當LM法用于（5-18）問題時，迭代公式為：

式中μ_k是LM參數，I為單位矩陣，{p^（k）（μ_k）}為搜索逼近（5-17）式解的校正向量，它依賴于參數μ_k值，控制搜索方向和長度。

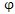
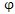
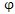
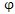
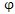
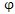
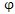
LM算法的優點是，在計算（5-20）式時，可以不考慮[J（{a^（k）}）]是否滿秩，μ_k可以起到 （{a}）下降參數的作用，{p^（k）（μ_k）}是 （{a}）在{a^（k）}處的下降方向，而且總存在這樣的μ≥0，使 （{a^（k）}+ p^（k））< {a^（k）}）（對所有k），隨著μ值的增大，{p^（k）（μ_k）}的方向越來越接近 （{a^（k）}的負梯度方向，此時，收斂速度變慢，但放寬了對初始近似{a^（0）}的要求。缺點是選擇μ滿足 （{a^（k+1）}）< （{a^（k）}）時，在一個迭代步驟中需要多次求解方程組（5-20），大大增加了計算量，因此有必要對LM法進行改進，以使選擇μ_k時即不增加太多的計算量，又能保證滿足下降性質，即有一定的收斂速度，又能改善（5-20）方程組的病態性。改進后的迭代公式為：

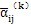
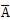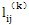
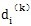
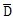式中才 為矩陣 ^（k）的元素。 ， 分別為矩陣L^（k）， ^（k）的元素。公式（5-23）和（5-27）和（5-28）中不含參數聲μ_k，因此改變μ_k時，只需重新計算(5-24),而不需要重新進行三角分解。顯然，改進后的算法減少了由于選擇合適的μ_k而帶來的計算量。這種算法與LM法的不同之處在于用正定矩陣L_k 代替了單位矩陣I，它不僅調整了矩陣 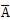^（k）的主對角元素，而且對整個矩陣進行了調整，它比LM法有更好的收斂速度。
為了得到合適的μ_k值，使得搜索向量{p^（k）（μ_k）}更快更好地滿足 （{a^（k）}+ p^（k））< {a^（k）}），加速收斂，改善LM法對初始值{a^（0）}要求過高的缺點，本文采用一種選擇合適μ_k值的新算法，對LM法進行了改進，選擇計算步驟如下：

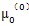
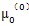
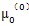
①.取定初始近似{a^（0）}和初始值 ，為了調整μ_k值，引人調整系數v, 可以取得小一些，取 =10^-2，v=5。

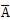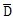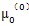
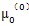
②.按（5-21) 式首先算得［J（{a^（0）}）]，然后按（5-26）式算得0⁽⁰⁾ ，再根據（5-27）、（5-28）式算得矩陣L^(0）和 ^（0）中的各元素，按(5-25）、(5-23）和（5-24）算得{P^（0）（ ）}；按（5-17）算得{r（{a^（0）}）}；按（5-18）算 （{a^（0）}）。并計算{a^（1）}={a^（0）}+{P^（0）（ ）}和 （{a^（1）}）
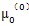
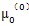
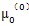
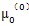
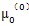
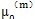
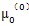
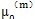
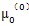
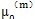
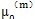
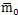
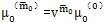
③.(l）如果少 （{a^（1）}）≤ （{a^（0）}），則以 /v代替 重新計算{P^（0）（ /v）}和新的{ ^（1）}， （{ ^（1）}）。（a）如果有 （{ ^（1）}）≤ （{a^（0）}），則取定μ₀= /v；（b）如果 （{a^（1）}）> （{a^（0）}），則取定μ₀= ，（2） （{a^（1）}）> （{a^（0）}），則需增大μ值，取 =v^m ，以 代替 ，逐次對m=1，2，…時的 代入（5-24）進行計算，最后取定使不等式 （{a^（0）}）+{ P^（0）（ ）}）< （{a^（0）}）成立的最小正整數 對應的 作為μ₀以及{a^（1）}+{P（ ）}。

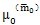
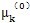
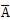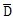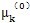
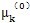
④.假定已求得第k次近似{ a^（k）}和相應的 =μ_k-1，算出[J（{ a^（k）}）]， ^（k），L^（k）， ^（k），r（{ a^（k）}）}， （{ a^（k）}），然后算得{P（ ）}，并計算{ a^（k+1）}={ a^（k）}+{P（ ）}和 （{ a^（k+1）}）。

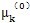
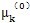
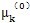
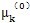
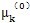
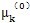
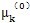
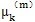
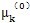
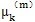
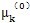
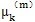
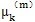
⑤.（1）如果 （{ a^（k+1）}）≤ （{ a^（k）}），則減少 以/V代替 重新計算{P（/V ）}和對應的{ ^（k+1）}及 （{ ^（k+1）}）（a）如果 （{ ^（k+1）}）≤ （{ a^（k）}），則取定μ_k=/V ；（b）如果 （{ ^（k+1）}）> （{ a^（k）}），則取定μ_k= （2）如果 （{ ^（k+1）}）> （{ a^（k）}），則增大 值，可取 =v^m ,以 代替 ,逐次時m=1，2，…時的 代入（5-24）式進行計算，最后取定使不定式 ({ a^（k）}+{P（ ）}< （{ a^（k）}）。

⑥.目標函數 （{a}）的k次迭代和k+1次迭代如果滿足絕對誤差和相對誤差精度，即可將{ a^（k+1）}作為近似解。如果不滿足，則以{ a^（k+1）}代替{ a^（k）}，μ_k代替μ_k-1去執行步驟⑤，直到滿足要求為止。

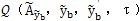
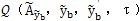
至此，（5-17）式的求解方法已經建立起來，日（5-17）式求解{a}還需要求出 ，{q}和（f_j）（j=1，2，…，n）。另外，在用（5-21）式求[J（{a}）]時遇到r_i（{a}）對隱含向量{a}求偏導數的麻煩，因此在計算[J（{a}）]時，需要做些處理。由（5-15）式可知，它是頻域內的2N+1個非線性代數方程組，而非線性遲滯恢復力 是時域函數，因此在求解（5-15）時需要進行頻域與時域相互變換，并做一些數學上的處理，下面逐一敘述。

5-3一步用SSGILM法計算帶有非線笥聯軸器軸系穩態響應

為了求得未知向量{a}，還需做以下工作：

一、向量函數{r（{ a^（k）}）}的計算

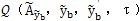
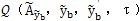
要計算{r（{ a^（k）}）}為聯軸器恢復力 的傅立葉級數展開式各簡諧分量的系數向量。對于給定的{ a^（k）}，不能由時域表達式求得頻域內的{q（{ a^（k）}）}，而必須按以下步驟計算。

首先，由給定的頻域向量{q（{ a^（k）}）}，根據 的N個時域離散值，記為Y（1）～Y（N）和DY（1）～DY（N），其次，由下式求得 幅值

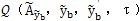
然后，將 以及 時域離散值代入第三章中得到的恢復力 的表達式（3-8）、（3-12）、（3-27）和（3-41）式，算得對應于{ a^（k）}的恢復力Q在一個周期內N個Q的時域離散值進行FFT變換，即可得到非線性恢復力Q在頻域內的各諧波分量的系數向量{q（{ a^（k）}）}

2. {f_j（{ a^（k）}）}的計算

{f_j（{ a^（k）}）}是式（5-6）中恢復力F_j的傅立葉級數展開式各諧波分量的系數向量。當向量{ a^（k）}給定時，首先由5-2節中所述方法算得各個 和 （j=1，2，…，n），其次由（5-6）式中恢復力F_j的各諧波分量的系數向量{f_j（{ a^（k）}）}。

算得{q（{ a^（k）}）}和{f_j（{ a^（k）}）}后，代入（5-15）式即可得到{r（{ a^（k）}）}。

二、雅可比矩陣[J（{ a^（k）}）]的計算

為計算方便起見，將雅可比矩陣式（5-21）分解成三個矩陣：

[J（{ a^（k）}）]=[J₁]+[J₂]+[J₃]                  （5-30）

1.[J₁]的計算

由（5-15）和（5-21）式可得：

[J₁]=

2. [J₂]的計算

[J₂]的計算實際上就是對 {q（{ a^（k）}）}/ { a^（k）}的計算。由于恢復力Q的函數表達式是{ a^（k）}的隱函數，因此不可能由Q的表達式直接進行FFT變換來求得{q（{ a^（k）}）}，也可能由{q（{ a^（k）}）}直接對{ a^（k）}；求偏導數來得到[J₂]：

由第三章中的式（3-8）、（3-12）、（3-41）和本章中的式（5-13）可得：

式中， ，， ，， 可以直接由Q的表達式和（5-13）進行解析計算得到， / { a^（k）}， / { a^（k）}也可以由（5-13）式直接進行解{ a^（k）}，選取增量△{ a^（k）}，然后計算一個周期內對應的 （{ a^（k）}+△{ a^（k）}）和 （{ a^（k）}）值，得：

由（5-32）式算得 / { a^（k）}的時域離散值后，進行FFT變換即可得到頻域中的 {q（{ a^（k）}）}/ { a^（k）}。

3. [J₃]的計算

[J₃]的計算實際上就是偏導數 {f_j（{ a^（k）}）}/ { a^（k）}的計算。計算方法與計算 {q（{ a^（k）}）}的方法類似，故不再贅述。對于[J₂]，[J₃]、分別有式（5-34）、（5-35）。

在計算出{r（{ a^（k）}）}和{J（{ a^（k）}）}之后，就可以按5-2節中發展的ILM法進行搜索迭代計算，由初始向量{a^（0）}不斷搜索逼近滿足精度要求的{ a^（k+1）}，然后代入（5-10）、（5-11）、（5-12）和（5-7）即可求得聯軸器從動動端質理塊m_b的穩態響應y_b以及軸系中各圓盤轉子穩態應Y。同時還可以得到對應的幅頻圖。

5-4小結
本章對帶有非線性聯抽器的n+1個自由度軸系在四盤質量偏心產生的激勵力作用下穩態響應計算方法進行了研究，以GLM法為基礎，提出了一種稱為SSG

ILM (Separate System-Ga1erkin and Imp-r0ved Leenberg-Marquardt的方法，用于計算局部具有非線性特性軸系的穩態響應，
主要工作如下：
1.建立帶有非線性聯鈾器n+1個自由度軸系的止）學模型和數學模型，為了求解這種局部含有非線性元件的軸系的穩態響應，將軸系分成兩個子系統，即含有n個自由度的線性軸系和含有非線性變參數的聯軸器子系統。
2.對線性軸系子系統運動微分方程組用正則坐標變換進行解藕處理；對非線性變參數的聯軸器子系統運動微分方程用Galerkin法，變成一組隱含系數向量{a}的非線性代數方程組。
3.針對LM法的缺點，采用已有的選擇合適μ值的方法和加快收斂速度的算法對LM法進行了改進，用改進算法對上面得到的非線生方程組中的未知向量{a}進行搜索計算，最后解出局都具有非線性特性軸系的穩態響應。