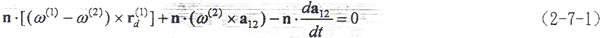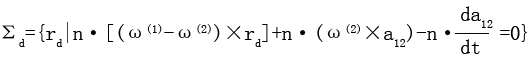第二章 彈性共軛曲面原理的研究
2.1 導言
彈性共軛曲面原理的研究是為了適應現代機械工業發展的需要,解決成對彈性體曲面的幾何圖形及其運動間的關系的問題。在機械制造和機械設計中,都存在共軛曲面問題,它們對加工質量和傳動性能都有非常大的影響。在有彈性變形時,共軛曲面的幾何圖形及其運動間的關系將與由剛性條件下得出的結果不同,從而不能滿足原來所設想的要求。尤其在剛性較差的零件加工和大柔性的傳動中,彈性變形對共軛關系的影響就更為重要。如在齒輪傳動方面,以往的輪齒修形的研究主要是針對多齒嚙合的嚙合齒對數變化的過渡狀態的。而在非多齒嚙合過渡狀態,由于變形的作用,共軛條件也會遭到破壞,尤其在大齒面和大柔性的傳動中,彈性變形的影響是不能忽略的。因此,這些修形的研究由于缺乏具有普遍意義的理論的指導,都存在一定的片面性。隨著機械加工向高精度、高效率的發展和機械傳動向大載荷、高性能的發展,迫切需要新的彈性共軛曲面理論作為指導,解決機械設計和機械制造中出現的彈性共軛曲面問題。
本文提出了彈性共軛曲面的基本理論,建立彈性共軛曲面運動基本方程,研究彈性共軛曲面的一般求解方法,為進一步深入全面地研究彈性共軛曲面問題奠定理論基礎。
2.2 彈性共軛曲面研究的前提假設
彈性共軛曲面原理的研究是一個復雜的問題,為了突出主要問題,因而忽略一些因素的影響,首先作出一些前提假設,而且本文只研究線接觸彈性共軛曲面問題。
1.所研究的變形是在彈性變形范圍,受力變形在作用力消除后完全恢復,即變形曲面的完全彈性體概念;
2.忽略接觸曲面間的相互摩擦作用,即忽略曲面上的切向力的作用;
3.不考慮熱變形;
4.彈性變形相對于曲面的相對運動無滯后。
2.3 彈性共軛曲面定義
彈性共軛曲面的定義是:兩彈性體在外力作用下產生彈性變形后,彼此既保持連續相切接觸,又不互相干涉,并且按給定運動規律運動的一對彈性變形恢復后的曲面。
一對彈性體曲面在外力作用下的運動規律與在彈性變形恢復狀態下幾何圖形間關系的研究就是彈性共軛曲面研究的內容。彈性共軛曲面是在受力變形下仍保持共軛運動規律的,它們在相互接觸的運動過程中幾何形狀是不斷變化的,是動態的過程,我們最終需要求解的彈性共軛曲面不是這一系列的動態的幾何圖形,而是利用這些動態的幾何圖形和它們的相對運動要求來求解在不受力變形狀態下的曲面幾何圖形及其運動關系。
根據上述彈性共軛曲面概念可知,一對彈性共軛曲面在外力作用下相互接觸產生彈性變形,接觸參考點處的兩曲面的速度矢量沿該點的公法線的投影應相等,有
v(1)·n=v(2)·n
即
v(12)·n=0
這就是彈性共軛曲面在相對運動時所應滿足的要求。
2.4 彈性共軛曲面的運動分析
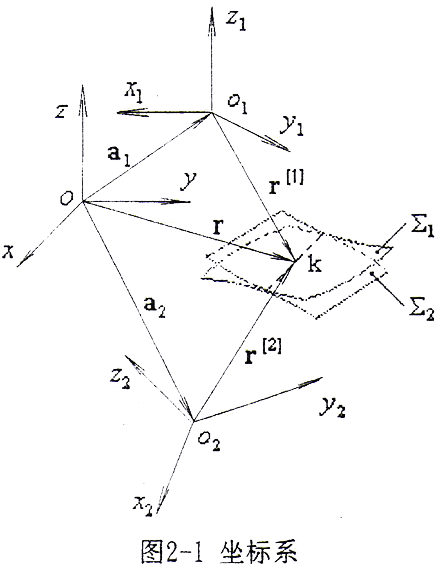
2.4.1 坐標系(如圖2-1所示)
坐標系S1(o1,x1,y1,z1):與曲面Σ1固連的動坐標系;
坐標系S2(o2,x2,y2,z2):與曲面Σ2固連的動坐標系;
坐標系S(o,x,y,z):靜坐標系;
設K點為兩曲面受力變形后的接觸參考點,a1、a2為靜坐標系S原點到兩動坐標系S1和S2原點的徑矢;r(1)、r(2)為Σ1、Σ2上K點在S1、S2坐標系的徑矢;r為K點在S坐標系的徑矢。
2.4.2 彈性體接觸參考點的運動分析
由圖2-1知
r=r(1)+a1
所以有
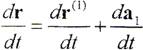
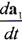 表示動坐標系S1的原點o1相對于靜坐標系S的運動速度矢量。
表示動坐標系S1的原點o1相對于靜坐標系S的運動速度矢量。
由于 r(1)=x1i1+y1j1+z1k1
所以
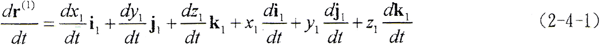
若為剛性曲面,則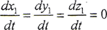 ,由于現在所研究的曲面為彈性曲面,接觸參考點在S1坐標系的徑矢將隨彈性變形而發生變化,因此,
,由于現在所研究的曲面為彈性曲面,接觸參考點在S1坐標系的徑矢將隨彈性變形而發生變化,因此,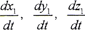 不恒等于零,令
不恒等于零,令
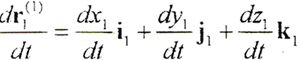
顯然它是Σ1上接觸參考點在S1坐標系的徑矢對時間的變化率,即接觸參考點相對于S1坐標系的速度矢量。
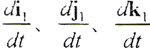 為S1坐標分量的單位矢量對時間的微分[2]。
為S1坐標分量的單位矢量對時間的微分[2]。
由i1⊥j1⊥k1
i1·j1=j1·k1=k1·i1=0有
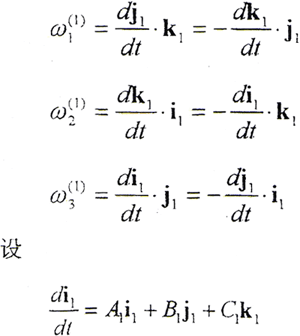
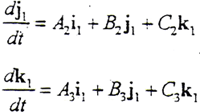
以i1、j1、k1分別點乘以上三式的兩邊,有
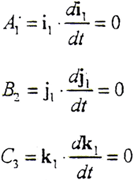
同理可得
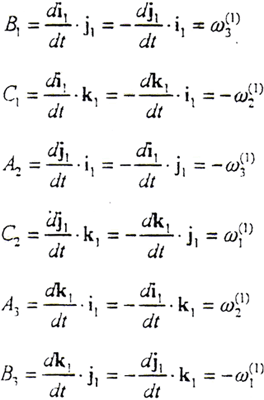
所以有

令 ω(1)=ω1(1)i1+ω2(1)j1+ω3(1)k1
而 r(1)=x1i1+y1j1+z1k1
則有
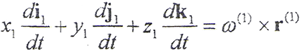
所以

式中ω(1)為S1坐標系的角速度矢量。
2.4.3 彈性體相對運動分析
由前推導知,Σ1上K點的相對于S坐標的速度
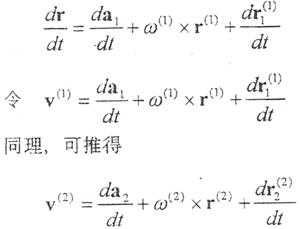
式中
r(2)=x2i2+y2j2+z2k2
ω(2)=ω1(2)i2+ω2(2)j2+ω3(2)k2
ω(2)為S2坐標系的角速度。
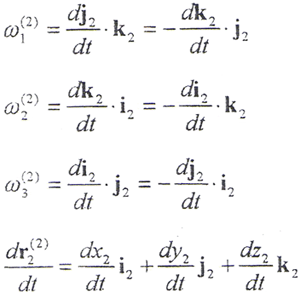
 包含坐標系S1、S2原點的運動速度和由變形使原點位置產生變化的速度。
包含坐標系S1、S2原點的運動速度和由變形使原點位置產生變化的速度。
所以,Σ1、Σ2在K點的相對速度
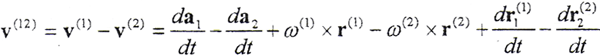
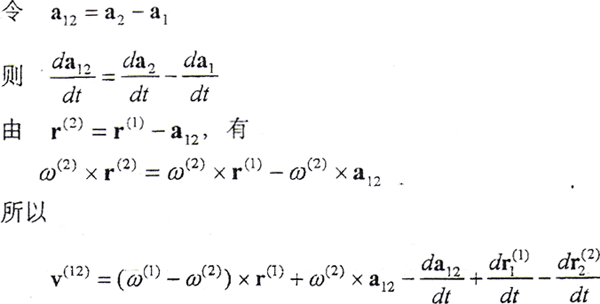
a12為坐標系S1原點至坐標系S2原點的矢量,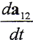 為坐標系S1、S2原點的相對運動速度矢量,它可包含兩共軛曲面支承件的彈性變形速度,
為坐標系S1、S2原點的相對運動速度矢量,它可包含兩共軛曲面支承件的彈性變形速度,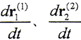 分別為曲面Σ1、Σ2上接觸參考點相對于坐標系S1、S2的彈性變形速度矢量。
分別為曲面Σ1、Σ2上接觸參考點相對于坐標系S1、S2的彈性變形速度矢量。
2.5 彈性共軛曲面運動基本方程
根據彈性共軛曲面在相對運動時所應滿足的條件
n·v(12)=0
即有
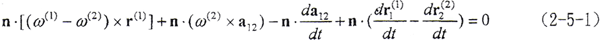
(2-5-1)式就是彈性共軛曲面運動基本方程。
若為剛性曲面,上式中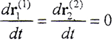 ,則可由(2-5-1)式得出傳統的剛性共軛曲面運動基本方程。由此可知,剛性共軛曲面只是彈性共軛曲面的特殊情況。
,則可由(2-5-1)式得出傳統的剛性共軛曲面運動基本方程。由此可知,剛性共軛曲面只是彈性共軛曲面的特殊情況。
(2-5-1)式中有三個運動矢量ω(1)、ω(2)、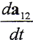 ,不同的共軛運動形式,其三個運動矢量方向都是確定的。在機械加工中,根據不同情況有不同的運動自由度,均可用以上三個運動矢量確定;在嚙合傳動中,最一般情況為相錯軸傳動,在定軸傳動中,如果不考慮軸系的變形,則
,不同的共軛運動形式,其三個運動矢量方向都是確定的。在機械加工中,根據不同情況有不同的運動自由度,均可用以上三個運動矢量確定;在嚙合傳動中,最一般情況為相錯軸傳動,在定軸傳動中,如果不考慮軸系的變形,則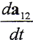 =0,(2-5-1)式成為
=0,(2-5-1)式成為
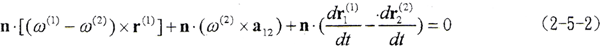
2.6 變形對接觸參考點法線方向的改變
由于變形的作用,接觸參考點的法線方向將發生一定的變化,以下分析在xoy平面內接觸參考點法線方向的改變量。
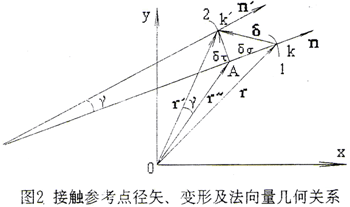
如圖2所示,變形前,曲面在位置1;變形后,曲面在位置2。變形前后接觸參考點為k、k′。變形前的接觸參考點徑矢及法線向量為r、n;變形后的接觸參考點徑矢及法線向量為r′、n′。設變形為δ,其切向分量和法向分量分別為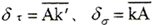 。變形前后的法線向量夾角為γ。r″為只產生法向變形后的接觸參考點徑矢。在小變形條件下,可認為只產生切向變形后的接觸參考點徑矢與法線向量的夾角不變,即r″與n的夾角等于r′與n′的夾角。由幾何關系有
。變形前后的法線向量夾角為γ。r″為只產生法向變形后的接觸參考點徑矢。在小變形條件下,可認為只產生切向變形后的接觸參考點徑矢與法線向量的夾角不變,即r″與n的夾角等于r′與n′的夾角。由幾何關系有

式中 ∠k′A0=3π/2-∠kA0
設r、n之間的夾角為ε,則有
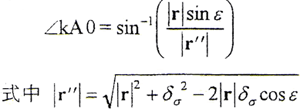
通常情況下,變形量相對于曲面參考點徑矢的大小為微小量,其切向分量更小,主要由撓曲變形引起。由(2-6-1)式知,γ值非常小。一般情況下,可忽略這一法線方向的改變,認為變形后的接觸參考點法線方向不變,以便于求解。
2.7 彈性共軛曲面的求解
2.7.1 求解思路
彈性共軛運動的過程,實質上是兩動態變形曲面互為包絡的過程,對變形過程中的曲面的描述是非常困難的,而我們所關心的是變形恢復狀態的曲面如何保證在一定的載荷作用下滿足變形條件的共軛運動規律,因此,可不去描述這個動態變曲面的全過程。
由(2-5-1)式知,它是r(1)、r(2)需滿足的微分方程。Σ1、Σ2在接觸的最初階段,接觸參考點在接觸力作用下,隨著Σ1、Σ2的相對運動,變形逐漸增大,在此階段,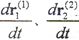 不為零。當接觸參考點變形達到最大時,該瞬間變形結束,回彈尚未開始,顯然,此瞬時
不為零。當接觸參考點變形達到最大時,該瞬間變形結束,回彈尚未開始,顯然,此瞬時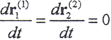 ,這時的接觸參考點為決定兩曲面運動關系的點,受力達到平衡,我們稱這樣的接觸參考點為變形最大點。將這樣的點之徑矢記為rd(1)、rd(2),(2-5-1)式就成為
,這時的接觸參考點為決定兩曲面運動關系的點,受力達到平衡,我們稱這樣的接觸參考點為變形最大點。將這樣的點之徑矢記為rd(1)、rd(2),(2-5-1)式就成為
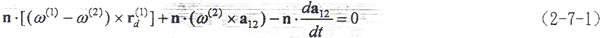
即變形最大點滿足條件(2-7-1)式。
與變形最大點相鄰的點,變形已經發生,但未達到最大,即使由于變形的關系已接觸,但這樣的點并不對兩曲面的運動起決定作用。當運動繼續,相鄰點成為變形最大點,原來的變形最大點則處于變形回彈狀態。整個連續的曲面之運動就是由無窮多個這樣的變形最大點所決定的,我們稱這無窮多個變形最大點的動坐標集合為變形基本共軛曲面,簡稱為變形基本曲面。
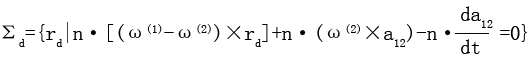
變形基本曲面為共軛運動過程中逐漸形成的,是由變形最大點所構成的假想曲面,它是求解彈性共軛曲面的過渡曲面。變形基本曲面在彈性變形恢復狀態所形成的曲面即為彈性共軛曲面。變形基本曲面及其運動關系確定后,則可根據不同的求解要求,求解彈性共軛曲面或求解運動規律。
由以上分析可以看出,彈性共軛曲面的求解,一個重要的問題是接觸參考點最大變形的求解。
2.7.2 變形的求解
彈性體的變形可認為是撓曲變形與接觸變形的迭加,設所求解的彈性共軛曲面邊界及作用在曲面上的作用力為已知,則變形即可求出。隨著數學力學的發展,變形的求解也日益精確[26][27][33][35][43][46~50][54~62]。有限元、邊界元方法成為求解變形的有力工具。本文不詳細討論變形的求解方法。
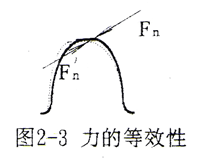
如圖2-3所示,變形的恢復可看成在受力變形狀態下加上一個與原作用力大小相等、方向相反的作用力。由于變形的微小性,可認為Fn與Fn′的變形效應相同,即Fn′作用下rd(i)的變形恢復量等于Fn作用下產生的變形量,也就是說變形恢復量可由在變形基本曲面上作用相同的力的變形量的計算來確定。
2.7.3 彈性共軛曲面的求解方法
當已知變形基本曲面和在特定載荷下的變形,則可求解彈性共軛曲面。
r(i)=rd(i)+δ(i)·n0(i) (i=1,2) (2-7-2)
式中
r(i)——參考點彈性共軛曲面徑矢
rd(i)——參考點變形基本曲面徑矢
δ(i)——參考點最大法向變形量
n0(i)——參考點單位法向矢量
彈性共軛曲面Σi即為所有離散點r(i)的集合。
Σi={r(i)|r(i)=rd(i)+δ(i)·n0(i)} (i=1,2)
上一頁
下一頁


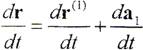
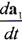 表示動坐標系S1的原點o1相對于靜坐標系S的運動速度矢量。
表示動坐標系S1的原點o1相對于靜坐標系S的運動速度矢量。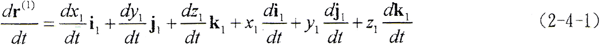
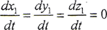 ,由于現在所研究的曲面為彈性曲面,接觸參考點在S1坐標系的徑矢將隨彈性變形而發生變化,因此,
,由于現在所研究的曲面為彈性曲面,接觸參考點在S1坐標系的徑矢將隨彈性變形而發生變化,因此,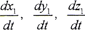 不恒等于零,令
不恒等于零,令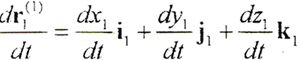
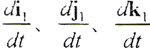 為S1坐標分量的單位矢量對時間的微分[2]。
為S1坐標分量的單位矢量對時間的微分[2]。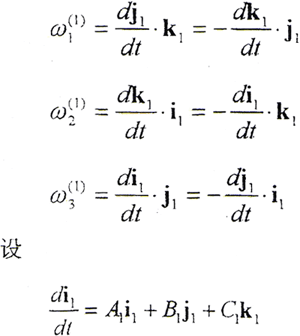
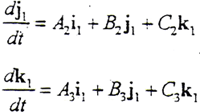
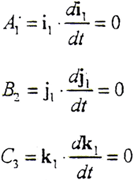
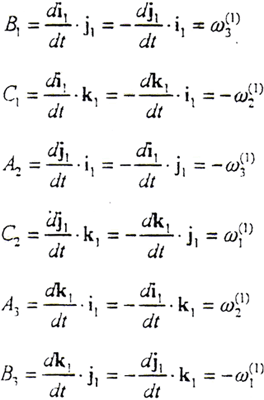

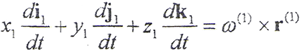

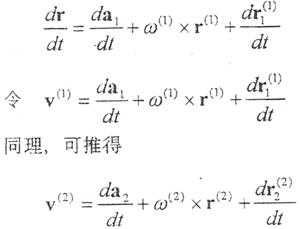
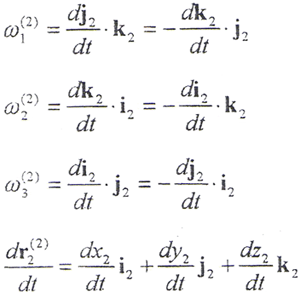
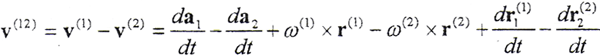
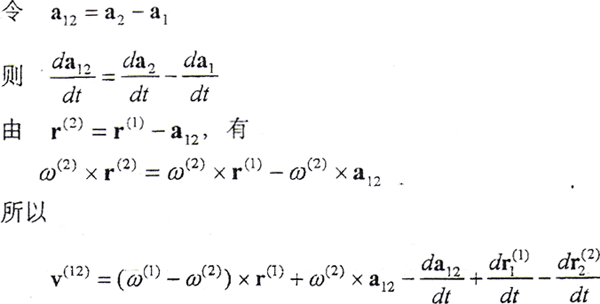
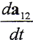 為坐標系S1、S2原點的相對運動速度矢量,它可包含兩共軛曲面支承件的彈性變形速度,
為坐標系S1、S2原點的相對運動速度矢量,它可包含兩共軛曲面支承件的彈性變形速度,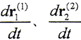 分別為曲面Σ1、Σ2上接觸參考點相對于坐標系S1、S2的彈性變形速度矢量。
分別為曲面Σ1、Σ2上接觸參考點相對于坐標系S1、S2的彈性變形速度矢量。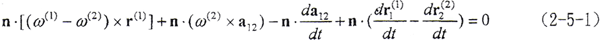
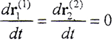 ,則可由(2-5-1)式得出傳統的剛性共軛曲面運動基本方程。由此可知,剛性共軛曲面只是彈性共軛曲面的特殊情況。
,則可由(2-5-1)式得出傳統的剛性共軛曲面運動基本方程。由此可知,剛性共軛曲面只是彈性共軛曲面的特殊情況。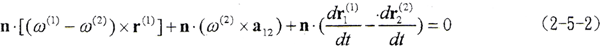

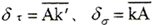 。變形前后的法線向量夾角為γ。r″為只產生法向變形后的接觸參考點徑矢。在小變形條件下,可認為只產生切向變形后的接觸參考點徑矢與法線向量的夾角不變,即r″與n的夾角等于r′與n′的夾角。由幾何關系有
。變形前后的法線向量夾角為γ。r″為只產生法向變形后的接觸參考點徑矢。在小變形條件下,可認為只產生切向變形后的接觸參考點徑矢與法線向量的夾角不變,即r″與n的夾角等于r′與n′的夾角。由幾何關系有
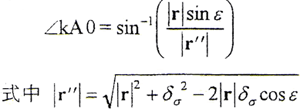
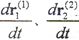 不為零。當接觸參考點變形達到最大時,該瞬間變形結束,回彈尚未開始,顯然,此瞬時
不為零。當接觸參考點變形達到最大時,該瞬間變形結束,回彈尚未開始,顯然,此瞬時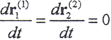 ,這時的接觸參考點為決定兩曲面運動關系的點,受力達到平衡,我們稱這樣的接觸參考點為變形最大點。將這樣的點之徑矢記為rd(1)、rd(2),(2-5-1)式就成為
,這時的接觸參考點為決定兩曲面運動關系的點,受力達到平衡,我們稱這樣的接觸參考點為變形最大點。將這樣的點之徑矢記為rd(1)、rd(2),(2-5-1)式就成為