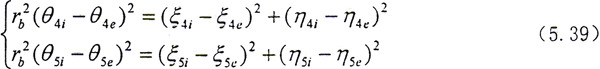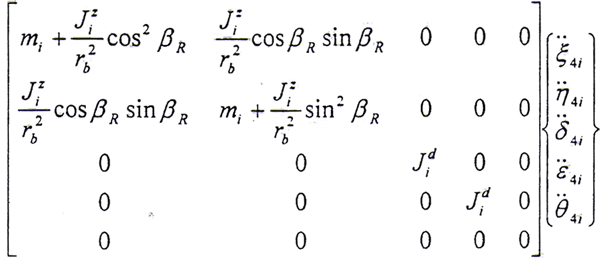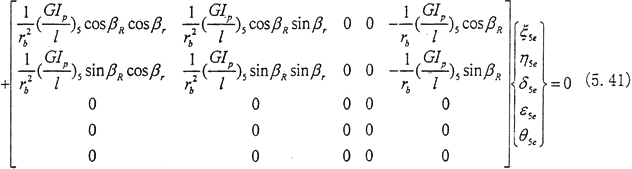5.4 彎扭耦合運動的討論
(1)在純扭轉情況下,由于內外齒輪的嚙合關系表現為傳動比是恒定的,即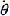 ji/
ji/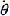 je=1.,雖然這個關系在山內進吾[32]、Marmol[34]和KANEMITSU[38]等人的研究中未曾明確指出,但實質上上式正是他們所處理的齒輪聯軸器系統振動問題的出發點,據此將扭轉振動和彎曲振動分開處理。
je=1.,雖然這個關系在山內進吾[32]、Marmol[34]和KANEMITSU[38]等人的研究中未曾明確指出,但實質上上式正是他們所處理的齒輪聯軸器系統振動問題的出發點,據此將扭轉振動和彎曲振動分開處理。
(2)在扭轉振動和彎曲振動同時發生時,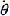 i與
i與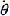 e的關系(參見式(5.11)或式(5.26))不再滿足上述關系。從分析力學的角度出發,這個關系實質上是對系統施加了一完整個約束。這個約束關系將表征齒輪扭轉的扭轉角和表征齒輪質心橫向運動的位移聯系了起來,正是這個關系才使得彎曲振動和扭轉振動耦合了起來。
e的關系(參見式(5.11)或式(5.26))不再滿足上述關系。從分析力學的角度出發,這個關系實質上是對系統施加了一完整個約束。這個約束關系將表征齒輪扭轉的扭轉角和表征齒輪質心橫向運動的位移聯系了起來,正是這個關系才使得彎曲振動和扭轉振動耦合了起來。
(3)從以上推導得的方程式(5.38)可知,軸承—轉子—齒輪聯軸器系統不僅在彈性項出現耦合,而且存在慣性耦合。從以上的約束關系不難想象,如果考慮了齒輪聯軸器的扭轉內阻尼,那么此時阻尼項也一定會出現彎扭耦合的現象。因此這是一典型的動力耦合問題。
(4)耦合不僅出現在所考慮的第j個結點上(包括內齒套、外齒輪),而且還影響到j+1個結點上,由于第j+1個結點又與第j+2個結點是耦合的,因此整個系統方程是全耦合的。
(5)雖然質量矩陣和剛度矩陣出現耦合,但在整體系統方程中在齒輪嚙合處仍呈現出對稱性,這與平行軸齒輪傳動系統[18]有所不同,在平行軸齒輪傳動系統中質量矩陣和剛度矩陣是非對稱的。彎扭耦合的慣性效應體現在對質量陣的修正上,修正項為Jjiz/rb2,設Jjiz=mjiρ2,其中ρ為內齒套的回轉半徑,一般而言內齒套的質量比外齒輪的質量要大許多,而且內齒套的質量又主要集中在外圈,因此ρ比rb要大,故Jjiz/rb2比mjk,(k=i,e)大得多,這樣對質量陣的修正非常明顯;彈性耦合由于齒對的剛度較大,而軸的扭轉剛度相對要小一些,因此對剛度陣的修正相對要小一些。
(6)彎扭耦合后,運動微分方程只在某些情況下可以進行線性分析,例如在滿足βR變化很小等條件,而在一般情況下系統方程則是非線性的,對此將在下一章中進行較深入的討論。如果將其寫成如式(5.38)所示的擬線性形式,則不僅剛度陣是廣義坐標的函數,而且質量陣也是廣義坐標的函數,這在轉子動力學中是比較少見的,因此在討論此類問題時就非常困難。傳統上在進行非線性分析時,往往將式(5.38)寫成“狀態方程”的形式,由于涉及到質量陣的求逆運算以及方程數目的成倍增加,所以計算工作量是比較大的。
在以往的彎扭耦合振動研究中[16,18,56,101,102,103],主要集中在以下二個方面:1)由于轉子系統的不平衡而產生的彎扭耦合現象[56,102]。2)具有外齒輪嚙合多平行軸的軸承—轉子系統中[16,18,101,103]。由于不平衡產生的彎扭耦合可以通過精細的平衡來消除,從理論上來講,平衡轉子不存在彎扭耦合。而在具有齒輪嚙合的多平行軸系統中,彎扭耦合是無法消除的,因此齒輪耦合逐漸成為研究的重點。通過上面的推導,可以發現彎扭耦合在軸承—轉子—齒輪聯軸器系統中同樣存在,而且耦合關系非常復雜,與具有齒輪耦合的多平行軸軸承—轉子系統相比,從結構上來看具有明顯的不同,在多平行軸的軸承—轉子系統中,各轉子平行布置一般比較短,扭轉剛度大,軸系的扭轉固有頻率比彎曲固有頻率大,此時彎曲振動是轉子振動的主要形式。但是在軸承—轉子—齒輪聯軸器系統中,系統由多個轉子串聯而成,因此整體系統的扭轉剛度成倍降低,軸系的扭轉振動問題愈顯突出,文獻[104]指出在過去的二十年中,在國內和國外均發生過由于扭振而出現大型機組被毀事件。這充分說明了這樣一個問題,扭轉振動已成為由聯軸器連接的軸承—轉子系統振動研究中一個不可缺少的內容。因此在軸承—轉子—齒輪聯軸器系統中進行彎扭耦合振動研究具有重要的實用價值。另外由于彎扭耦合作用,可以對以前未被發現和雖然在實際系統中存在但用傳統理論無法解釋的振動現象進行深入地研究,以便為此類系統的設計和故障診斷提供必要的理論依據。
5.5 軸承—轉子—齒輪聯軸器系統的彎扭耦合運動方程
以上我們建立了半聯軸器系統的運動方程,而在實際系統中往往是由二對內外齒輪同時嚙合傳動(例如CL和CLZ型齒輪聯軸器),軸承—轉子—齒輪聯軸器系統如圖5.5所示。
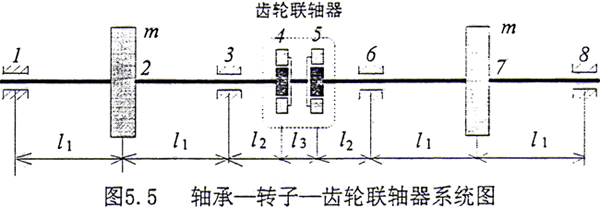
以上系統中有兩個半聯軸器組成,從上一節的推導中,可以看出在系統中存在二個約束方程,因此系統的自由度數要減少二個。對于圖5.5所示系統,在結點4和結點5存在齒輪嚙合,因此約束方程為
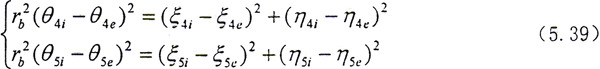
在式(5.27)和式(5.28)中,由于包含了θj+1(即為圖5.5中的θ5i)。而θ5i又必須要滿足以上的約束關系,所以可以想象在考慮了二個半聯軸器后,耦合關系更為復雜。但處理的方法是類同的,具體過程在此不再重復了。整個系統有8個結點,共48個自由度。下面僅列出結點4處的運動微分方程。
結點4外齒輪處


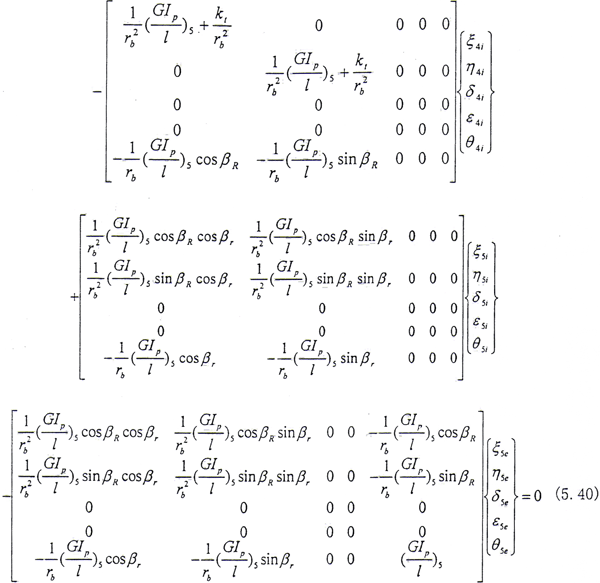
結點4內齒套處
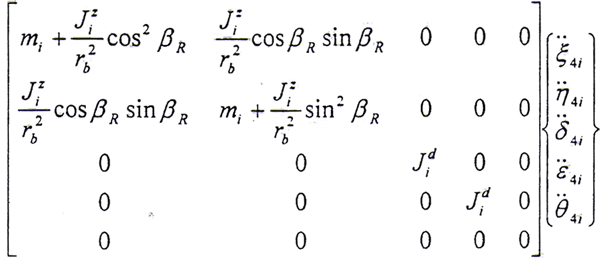
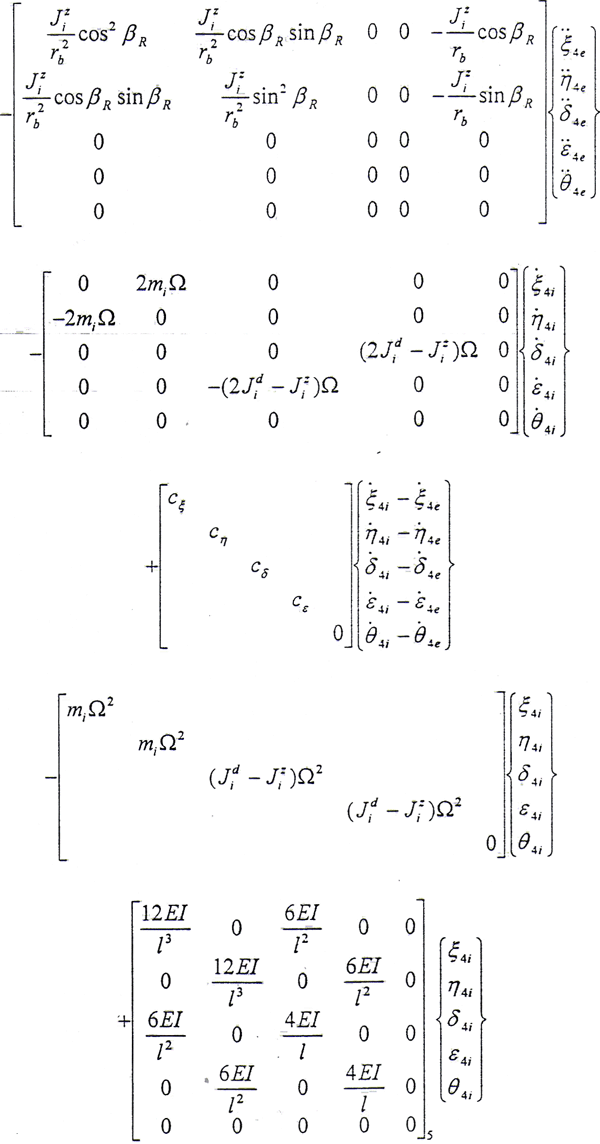
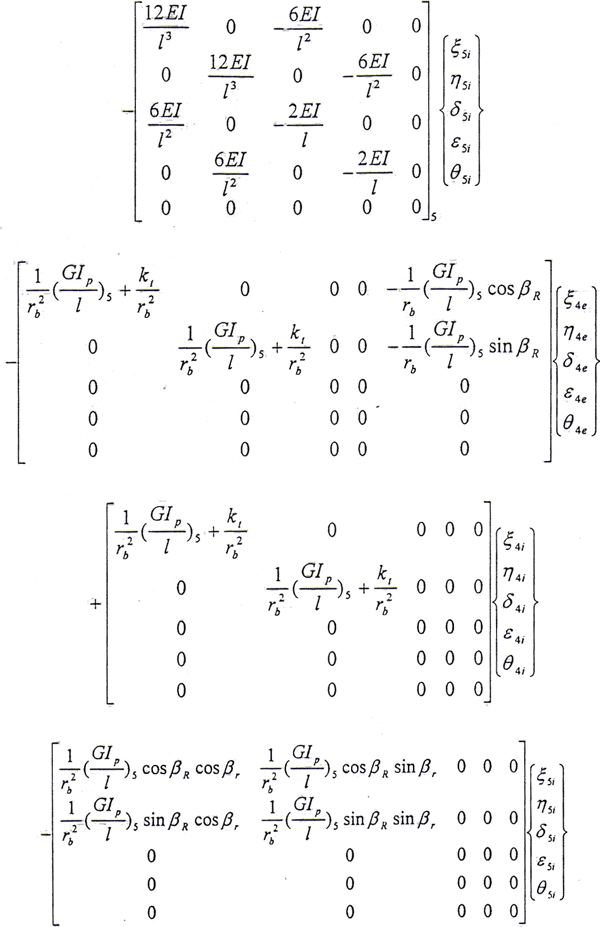
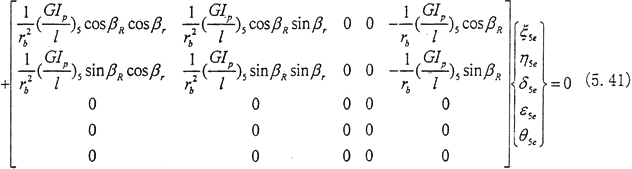
同理可以寫出結點5內外齒輪處的運動微分方程,在此從略。
5.6 小結
本章討論了在聯軸器內外齒輪軸線出現不對中或產生動態偏移時,軸承—轉子—齒輪聯軸器系統的彎扭耦合運動方程的建立過程,并對彎扭耦合進行了簡單的分析,主要的工作和結論如下:
(1)根據內、外齒輪的齒面方程和不脫齒的嚙合條件,推導了齒輪聯軸器的約束方程,這一約束方程體現了彎曲(或橫向)位移和扭轉擾動角之間的耦合關系。
(2)由拉格朗日方程,在旋轉坐標系中建立了半聯軸器的彎扭耦合運動方程,并闡述了軸承—轉子—齒輪聯軸器系統方程的建立過程。
(3)彎扭耦合后,系統不僅存在彈性耦合而且存在慣性耦合,但在整體系統的運動微分方程仍然具有對稱性。
(4)建立了CL型齒輪聯軸器系統的彎扭耦合運動方程,為深入探討具有齒輪聯軸器連接的軸承—轉子系統的動力學行為作了理論準備。
上一頁
下一頁

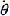 ji/
ji/